SUMA Y RESTA DE ANGULOS
Para efectuar las operaciones de suma y resta con las medidas de ángulos, sólo debe señalarse especialmente que deberá tenerse presente la relación existente entre los grados, minutos y segundos. Así por ejemplo al efectuar la suma, los minutos suman 81 y cabe separar 60, que constituyen un grado, que se agrega a los 41°:
Análogamente en una resta, si el número de minutos o segundos del minuendo es menor que los del sustraendo, se reducen unidades de orden superior (grados o minutos respectivamente), tal como lo indica el ejemplo. 1' de los 15' reducido a segundos y agregados a los 23" da 83" y restados 41" da 42". 1° de los 93° agregado a los 14' restantes da 74' y restados 38' quedan 36':
Se dice que un cuerpo se ve bajo un ángulo a, cuando el ángulo formado por las visuales dirigidas a los extremos del cuerpo es igual a a. Estos ángulos visuales varían no sólo con el tamaño del cuerpo, sino también con su distancia al observador. Así se pueden determinar los ángulos visuales bajo los cuales se ven edificios lejanos, personas, etc. Conociendo la distancia que separa del objeto se puede calcular la altura, o también conociendo la altura, calcular la distancia.
martes, 31 de marzo de 2015
MATEMATICA – Geometría elemental
lunes, 30 de marzo de 2015
MATEMATICA – Geometría elemental
SEGMENTOS, ANGULOS, CIRCUNFERENCIA: NOMENCLATURA
Dados varios puntos A, B, C, D, E tienen claro sentido las denominaciones usuales:
Recta AE, determinada por dos puntos A, E. Segmento AB, parte de recta limitada por dos puntos A, B llamados extremos. Semirrecta de origen B que contiene a C; semirrecta de origen D que no contiene a E. Angulo ABC, parte de plano limitada por dos semirrectas con el mismo origen B. Línea poligonal EABC. Los ángulos EAB y ABC que aparecen en la figura son ángulos convexos, pero hay otros tipos de ángulos: cóncavos, y llanos.
Dos ángulos se dicen iguales cuando por un movimiento del plano se pueden hacer coincidir uno con otro. Es evidente que todos los ángulos llanos son iguales.
El conjunto de los puntos de un plano cuya distancia a un punto O de éste es igual a un segmento r, se llama circunferencia de centro O y radio r. El punto O se llama centro, los puntos que distan de O menos que r se llaman puntos interiores y los que distan más se llaman puntos exteriores. El diámetro está constituido por dos radios pertenecientes a semirrectas opuestas. Cuerda es el segmento que une dos puntos de la circunferencia y secante es toda recta que corta a la circunferencia. Círculo es el conjunto de los puntos interiores de una circunferencia. El ángulo cuyo vértice está en el centro se llama ángulo central y determina sobre la circunferencia un arco. La parte de círculo correspondiente a un ángulo central es un sector circular y la parte de círculo comprendida entre la circunferencia y una cuerda es un segmento circular.
domingo, 29 de marzo de 2015
MATEMATICA – Cuerpos geométricos
LA RELACION DE EULER
Consignemos en un cuadro los números correspondientes a caras c, aristas a y vértices v de los cinco poliedros regulares:
En el caso del tetraedro:
c + v —a = 2
Lo mismo ocurre con todos estos poliedros. Esta notable propiedad, que no parece haber sido conocida por los griegos, fue descubierta por Descartes y luego, independientemente, por Euler. Más notable es el hecho de que vale no sólo para los poliedros regulares, sino para todos los poliedros simples, es decir para los sólidos cuya superficie está constituida por un número cualquiera de polígonos (regulares o no, del mismo o distinto número de lados).
sábado, 28 de marzo de 2015
MATEMATICA – Geometría elemental
LAS RECTAS PARALELAS
Dos rectas de un plano que no tienen ningún punto común se llaman paralelas y se escribe: a//b.
POSTULADO V DE EUCLIDES: Por un punto exterior a una recta pasa una paralela a dicha recta y una sola. Durante mucho tiempo se discutió si esta proposición se podía o no demostrar. Pero cuando el matemático húngaro Bolyai (1802-1860) y el matemático ruso Lobatchevsky (1793-1856) construyeron geometrías en las que no era válida la proposición de Euclides, quedó demostrado que esa proposición tenía carácter de postulado independiente de los otros. Si se acepta, conduce a la geometría clásica de los Elementos de Euclides y si no se acepta lleva a la construcción de las geometrías no-euclidianas; muy poco podremos decir de ellas en la parte de Geometría moderna.
Si una recta t corta a dos paralelas se forman ocho ángulos. Angulos tales como el 1 y el 5 ó el 4 y el 8 se llaman correspondientes. Se llaman alternos internos los ángulos 3 y 5, así como 4 y 6, y ángulos alternos externos 2 y 8, 1 y 7. Puede demostrarse que los cuatro ángulos agudos son iguales y también son iguales los cuatro obtusos.
viernes, 27 de marzo de 2015
MATEMATICA – Cuerpos geométricos
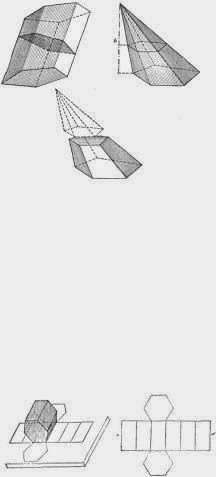
PRISMAS Y PIRAMIDES
Entre los cuerpos poliedros (es decir sólidos limitados por polígonos) los más comunes son los prismas, las pirámides y los troncos de pirámides.
El prisma se caracteriza por estar limitadopor dos polígonos iguales situados en planos paralelos, y por tantos paralelogramos cuantos lados tienen esos polígonos, mientras que la pirámide se obtiene atravesando un ángulo poliedro con un plano que corte todas las aristas. En la figura que representa el prisma se ha señalado especialmente la sección que se obtiene con un plano perpendicular a las aristas, y que se denomina sección normal del prisma. En la pirámide se ha señalado su altura, o distancia del vértice al plano de la base, y una sección con un plano paralelo a la base.
En particular si las aristas del prisma son perpendiculares a los planos de las bases se tiene un prisma recto, cuya construcción es muy sencilla, como lo explicala figura. Las caras laterales del prisma forman un rectángulo cuya base es la suma de los lados del polígono que sirve de base del cuerpo y cuya altura es la misma que la del cuerpo.
Si el polígono que sirve de base a la pirámide es regular y las aristas laterales son iguales, la pirámide se llama regular. El desarrollo de la pirámide está representado en la figura, en la que también se ve que los triángulos isósceles que forman las caras laterales tienen como altura un segmento que se llama apotema de la pirámide.
Si se corta una pirámide regular por un plano paralelo a la basese obtiene un tronco de pirámide regular. El desarrollo del tronco de pirámide está constituido, como se ve en la figura, por una serie de trapecios.
jueves, 26 de marzo de 2015
MATEMATICA - Ecuaciones y sistemas de primer grado
PRINCIPIOS GENERALES PARA LA RESOLUCION DE UNA ECUACION CON UNA INCOGNITA Una vez expresado algebraicamente el problema, esto es, una vez planteada la ecuación, los principios generales que han de guiarnos son los siguientes:
a) Todo término que se encuentra en un miembro de una ecuación se puede trasponer al otro miembro con signo cambiado.
b) Todo factor o divisor no nulo de un miembro de una ecuación se puede trasponer al otro como divisor o factor, respectivamente.
miércoles, 25 de marzo de 2015
MATEMATICA - Ecuaciones y sistemas de primer grado
LA NOTACION LITERAL Y LAS ECUACIONES
Cuando escribimos 3 + 5 = 5 + 3 y observamos que el orden de los sumandos no altera la suma, expresamos una verdad particular, que se puede verificar. Sentido diferente tiene el escribir:
a + b = b + a
Siendo a y b números cualesquiera, porque entonces ésta es una verdad universal, independiente de tal o cual número particular. Tales igualdades válidas para todos los valores de las letras que en ella figuran se llaman identidades. He aquí varias identidades importantísimas que aparecen en el comienzo del Algebra:
(a + b) ² = a² + 2ab + b²
Enunciado: El cuadrado de la suma de dos números es igual a la suma de los cuadrados de esos números más el doble del producto de los mismos. La segunda identidad:
(a + b) (a — b) = a² — b²
Se enuncia así: La suma por la diferencia de dos números es igual a la diferencia de sus cuadrados. Análogamente:
(a — b)² = a² —2ab + b²
La utilización de letras en los cálculos permite dar a la ciencia una gran generalidad y no debe considerarse a la notación literal como un formalismo accesorio, sino como la esencia del Algebra. Cuando decimos, por ejemplo, que el interés de cualquier capital C al cabo de un tiempo arbitrario t, al tanto por ciento i, está dado por la fórmula:
I = C.i.t/100
Tenemos compendiada en una sola expresión todos los casos posibles; y cuando se trata de saber, por ejemplo, cuál es el interés que producen 5.000 pesos al 4 % al cabo de 3 años, no hay más que reemplazar ordenadamente estos valores en la fórmula y así se obtiene I = 600 pesos. ¿Cómo sería posible compendiar infinitas fórmulas en una sola, si no fuera por la notación literal?
Ahora, ¿cuál es entonces el campo propio de esta creación hindú? Suele decirse que las ecuaciones.
Definición: Toda igualdad que relaciona un número desconocido x llamado incógnita, con ciertos datos o números conocidos, imponiéndole a aquél esta condición, se llama ecuación. El cálculo del cociente equivale, pues, a la resolución de ecuaciones del tipo bx =a y el cálculo de la diferencia a las de tipo b + x =a.
martes, 24 de marzo de 2015
MATEMATICA - Ecuaciones y sistemas de primer grado
EL METODO ALGEBRAICO
Cuando nos proponemos resolver algebraicamente un problema, debemos comenzar por suponer conocidos los valores de las incógnitas (que generalmente se designan con las letras x, y, z). Luego debemos escribir la igualdad o igualdades que el enunciado del problema impone entre esas incógnitas con otros datos conocidos. Así queda planteada la ecuación del problema. Luego se resuelve esta ecuación, es decir, se determinan con los recursos del Algebra, los valores numéricos de x, y, z ... que reemplazados en las ecuaciones hacen que los números que resultan en los dos miembros sean iguales. Finalmente se comprueba si los valores numéricos hallados satisfacen realmente las condiciones del problema propuesto. Un ejemplo muy sencillo aclarará la diferencia esencial entre el método aritmético y el método algebraico. Un padre tiene 40 años y un hijo 16. ¿Dentro de cuántos años la edad del padre será doble de la edad del hijo? Elegimos como incógnita x el número de años que han de transcurrir para que se verifique la condición exigida por el problema. Al cabo de los x años el padre tendrá 40 + x años y el hijo 16 + x, y la condición del duplo de la edad se expresa algebraicamente por la ecuación
2 (16 + x) = 40 + x
Pronto veremos cuán sencillamente se calcula la incógnita x, o se despeja la x, o se resuelve la ecuación. Si se busca en la ARITMETICA alguna regla o pauta para resolver este problema, no se la encontrará. Esa disciplina sólo estudia media docena de operaciones entre las infinitas que pueden proponerse. Así, por ejemplo: estudia la raíz cuadrada y la cúbica, es decir resuelve las ecuaciones de los tipos x² = a, x³ = a, pero no, por ejemplo, las del tipo x² + x³ = a. Este y todos los infinitos tipos posibles entran en el Algebra, ciencia que no es, como vemos, sino una prolongación natural de la Aritmética.
lunes, 23 de marzo de 2015
MATEMATICA - Ecuaciones y sistemas de primer grado
EL MAS ANTIGUO SISTEMA DE ECUACIONES
Hace casi 4.000 años el sacerdote egipcio A'h-mosé escribió un papiro didáctico de Aritmética y Geometría que suele llamarse papiro Rhind o Manual de A'h-mosé, en el cual figuran una serie de cálculos y problemas de gran interés matemático. Particularmente notable es el problema n° 40, cuyo enunciado original es el siguiente: "100 panes entre 5 personas; 1/7 de los 3 primeros es la parte de los 2 últimos; ¿cuál es la diferencia?", y que traducido a nuestra nomenclatura actual se enunciaría así: "Repartir 100 panes entre 5 personas, de modo que las partes sean regularmente crecientes (o estén en progresión aritmética) de modo tal que la suma de las dos menores sea la séptima parte de la suma de las tres mayores."
Es notable cómo los egipcios podían resolver con medios tan primitivos como los que poseían, un problema que actualmente analizaríamos así:
Sea x el primer número e y la diferencia constante entre los números sucesivamente crecientes. Las condiciones exigidas son dos:
x + (x + y) + (x + 2y) + (x + 3y) + (x + 4y) = 100 x + (x + y) = 1/7 . [(x + 2y) + (x + 3y) + (x +4y)]
Sistema de dos ecuaciones con dos incógnitas x, y muy sencillo de resolver con la técnica hoy usual. En efecto, las dos ecuaciones se pueden escribir:
5x + 10y = 100 (2x + y) 7 = 3x + 9y
En la primera ecuación se pueden dividir los dos miembros por 5 y queda:
x + 2y = 20 o sea x = 20 —2y
Sustituyendo este valor en la segunda ecuación en la cual hemos desarrollado el producto indicado en el primer miembro, tenemos:
14 (20 — 2y) + 7y = 3 (20 — 2y) + 9y
O sea:
280 — 28y + 7y = 60— 6y + 9y
Agrupando todos los números en el primer miembro y los que contienen a y en el segundo, se tiene:
280— 60 = 28y — 7y — 6y + 9y
220 = 24y y = 220/24 = 55/6
Como era x = 20 —2y resulta sustituyendo y por 55/6.
x = 5/6
La progresión buscada será:
5/3 ; 65/6 ; 20 ; 175/6 ; 115/3
domingo, 22 de marzo de 2015
MATEMATICA - Ecuaciones y sistemas de primer grado
INTERPRETACION GEOMETRICA DE LAS TRES IDENTIDADES NOTABLES
Si interpretamos las letras a y b que aparecen en las identidades como segmentos, es claro que los productos de segmentos los podremos interpretar como rectángulos y en particular las segundas potencias (cuadrados) como cuadrados. Por consiguiente construyamos los cuadrados de (a + b), (a--b) y el rectángulo (a + b) (a —b).
Los cuadrados de a y b y los dos rectángulos a.b muestran claramente que:
(a + b)² = a² + 2ab + b²
La segunda figura muestra que si al cuadrado de a le restamos dos rectángulos a.b, habrá que agregarle el cuadrado de b para obtener el cuadrado de (a — b):
(a — b)² = a² —2ab + b²
Finalmente la figura que sigue, muestra que siendo los rectángulos rayados iguales, si al cuadrado de a se le quita el cuadrado de b, se obtiene el rectángulo (a + b) (a — b) igual a²— b².
sábado, 21 de marzo de 2015
MATEMATICA - Ecuaciones y sistemas de primer grado
COMPARACION DE LOS DOS METODOS
La resolución algebraica de los problemas exige menor esfuerzo mental y suele ser más sencilla que la solución aritmética. Sin embargo, no hay que dejarse dominar por la rutina y querer forzar la resolución de todos los problemas mediante el planteamiento de la ecuación correspondiente. En muchos casos la solución aritmética es más elegante y natural. Veamos un ejemplo en el siguiente problema:
Un hortelano lleva manzanas; encuentra tres hombres, da al primero la mitad de las manzanas más 2; al segundo la mitad de las que le quedan más 2 y al tercero la mitad de las sobrantes más 2. Le queda una. ¿Cuántas manzanas llevaba? Planteado algebraicamente, elegimos como incógnita x la cantidad de manzanas. Entrega primero x/2 + 2 manzanas y le quedan por tanto x/2 — 2 manzanas y así sucesivamente llegamos- a la ecuación:
Resuelta esta ecuación se obtiene el resultado x = 36. Utilizando en cambio procedimientos aritméticos razonaríamos así: Antes de hallar al último hombre tenía el doble de (1 + 2) manzanas, es decir tenía 6. Antes de hallar al segundo tenía el doble de (6 + 2) es decir 16. Y antes de hallar al primero tenía 2 (16 + 2) = 36 manzanas.
viernes, 20 de marzo de 2015
MATEMATICA – Cuerpos geométricos
LOS POLIEDROS REGULARES, Y LAS LEYES PLANETARIAS DE KEPLER
En 1596 el inmortal Kepler formuló su célebre ley que permite localizar los planetas que giran alrededor del Sol, en la siguiente forma: "En una esfera, cuyo radio fuera igual al de la órbita de Mercurio, se circunscribe el octaedro; la esfera circunscrita a este sólido regular tendrá un radio igual al de la órbita de Venus. "A esta segunda esfera se circunscribe un icosaedro; la esfera circunscrita a este sólido tendrá un radio igual al de la órbita de la Tierra. "A esta tercer esfera se circunscribe un dodecaedro; la esfera circunscrita a este sólido tendrá un radio igual al de la órbita de Marte. "A esta cuarta, un tetraedro, y la esfera circunscrita que pasará por todas las cimas de este sólido tendrá por radio el de la órbita de Júpiter. "A esta quinta esfera se circunscribe un exaedro; la esfera que pase por todas las cimas de los ángulos de este sólido, es decir, la esfera circunscrita, dará el radio de la órbita de Saturno." Aun cuando esta formulación de Kepler no es correcta y sólo en 1609 en su Astronomía Nova expresó su ley definitivamente, sorprenden las relaciones geométricas encontradas por el sabio, que adicto a las doctrinas pitagóricas trataba de llevar la expresión de las leyes naturales a las formulaciones aritmético-geométricas, y aun a las concepciones sobre las armonías. Así, decía Kepler que "en la música de los cuerpos celestes, Saturno y Júpiter hacen el bajo; Marte el tenor; la Tierra y Venus el contralto y Mercurio el falsete".
jueves, 19 de marzo de 2015
MATEMATICA - Topología elemental
TOPOLOGIA DEL PLANO PROYECTIVO Y SUPERFICIES UNILATERAS
Otra falta de correlación entre plano (conjunto de puntos) y radiación (conjunto de rayos por un vértice) en la Geometría elemental es ésta: el plano tiene dos caras y la radiación una cara. Si esta página se embadurna de negro y se supone prolongada la hoja de papel y continuado indefinidamente su embadurnamiento, el plano tendrá una cara negra y otra blanca, pero si en la radiación o en el haz queremos pintar la mitad de cada rayo y seguimos avanzando, resultan pintados de negro los rayos que habíamos dejado blancos. Esto se expresa diciendo: la recta y el plano elemental son biláteros y el haz y la radiación son uniláteros. En la Geometría proyectiva desaparece esta diferencia: el plano proyectivoes unilátero, como la radiación. Comenzaremos por el ángulo completo.
Las letras A y B designan los dos puntos impropios y es preciso imaginar soldado el segmento impropio AB de la derecha con el de la izquierda, pero no como si se doblara el papel, pues entonces B caería sobre A; es preciso retorcerlo a la vez que se arquea, a fin de que coincidan las dos letras B y a su vez las dos A. Debe recortarse un ángulo como el de la figura y efectuar esta soldadura pintando o rayando como en la figura hacia la derecha y prosiguiendo por la izquierda quedará rayada por debajo (se ha indicado con rayas punteadas como si se traslucieran del otro lado). Hasta aquí nada hay de sorprendente, pues el ángulo parece tener dos caras; una rayada y otra no. Pero si ahora consideramos una hipérbola y comenzamos el rayado hacia la derecha como antes, prosiguiéndolo por la izquierda al avanzar más y más, resulta que estamos embadurnando debajo de lo ya pintado y así prosiguiendo quedará la tira de papel totalmente pintada, y lo que creíamos dos caras era una sola, pues de un punto se llega a cualquier otro sin atravesar el contorno.
Se comprueba que si bien esta tira de plano proyectivo es unilátera, el resto es bilátera.
miércoles, 18 de marzo de 2015
ARITMETICA - Introducción a la teoría de los números
MULTIPLOS Y DIVISORES Por ejemplo, si nos preguntan: ¿Pueden formar 27 soldados una columna de a 4? Contestaremos negativamente, pues sabemos que la división 27 : 4 no es exacta.
Vamos a estudiar la división prescindiendo del cociente; es decir, elegido un divisor d vamos a clasificar los números en divisibles y no divisibles por d. Un número a es divisible por otro d cuando la división a : d es exacta, y no divisible en caso contrario. También se dice en el primer caso que a es múltiplo de d, porque es el producto de d por otro número (el cociente que no interesa); o también, inversamente, que d es divisor o submúltiplo de a, o que divide al número a. Los múltiplos de 2 se llaman números pares, y los que no son múltiplos se llaman impares; al dividirlos por 2 dan resto 1.
MULTIPLOS DE 10 Y DE SUS POTENCIAS. — El resto de la división de un número cualquiera por 10 es precisamente la cifra de las unidades; por tanto: Un número es divisible por 10 solamente cuando termina en cero. Análogamente: Un número es múltiplo de 100, 1000, solamente cuando termina en dos, tres, ... , ceros respectivamente.
PROPIEDADES. — Si juntamos varios pelotones o compañías de soldados, para cada uno de los cuales es posible la formación en un número exacto de filas de a 4, el pelotón o compañía total podría formar también de a 4. En general si
a = d.q b = d.q'
Sumando es
a + b = d (q + q')
La suma de varios múltiplos de un número es también un múltiplo de este número. Además si:
a = d.q pa = d.pq
El producto de un múltiplo de un número por cualquier factor es también múltiplo de dicho número.
Análogamente a lo dicho para la suma podemos afirmar: La diferencia de dos múltiplos de un número es también un múltiplo de este número. De otro modo, por definición de la resta: Si un número divide a una suma de dos sumandos y a uno de ellos, también divide al otro.
martes, 17 de marzo de 2015
ARITMETICA - Introducción a la teoría de los números
MULTIPLOS COMUNES A VARIOS NUMEROS: MINIMO COMUN MULTIPLO
La teoría es parecida a la del m.c.d. Según hemos visto todo múltiplo de un número tiene todos los factores de éste elevados a iguales o mayores exponentes. Si se nos dan varios números:
2520 = 2³ . 3² . 5 . 7 900 = 2² . 3². 5² 2970=2 . 3³ . 5 . 11
y se nos pide la determinación de múltiplos comunes a todos ellos, bastará tomar todos los factores comunes y no comunes sin excepción y elevarlos cada uno a un exponente que no sea inferior al que tiene en ninguno de los números dados. Así, en el ejemplo planteado, cualquier producto conteniendo todos los factores 2, 3, 5, 7, 11 con exponentes no inferiores a los de 2³, 3³, 5², 7, 11, dará un múltiplo común a los números dados. Multiplicando, pues, estas potencias, que son las mayores de cada factor primo de los contenidos en los números dados, obtendremos el menor múltiplo común, llamado, según costumbre, mínimo común múltiplo y representado por la abreviatura m.c.m.
Cuando un número es múltiplo de otros varios, dicho número es el m.c.m. de todos ellos.
lunes, 16 de marzo de 2015
ARITMETICA - Introducción a la teoría de los números
EVOLUCION DE LA TEORIA DE LOS NUMEROS
Toda la teoría expuesta, así como la notable demostración de que la serie de números primos es ilimitada, se encuentra ya en los famosos Elementos de Euclides, genio matemático griego que vivió unos tres siglos antes que Jesucristo. Ello demuestra la atención prestada por los griegos a la teoría de los números, que dejaron completamente organizada en su parte elemental. Para ulteriores progresos es preciso llegar a los matemáticos del siglo XVII (Fermat, Euler, …) que iniciaron una serie de teorías, en las que hay problemas aún no resueltos. Los antiguos egipcios y griegos conocían ya la clasificación de los números en pares e impares. Los hindúes conocieron la divisibilidad por 3 y por 9, y es de presumir que, como autores del sistema decimal, supieron distinguir rápidamente los múltiplos de 5, 4, 25, etc. El carácter de divisibilidad por 11, no aparece en la historia matemática hasta el siglo XVII: súmense las cifras de lugar par, súmense las de lugar impar; ambas sumas deben diferir en un múltiplo de 11. Menos útiles todavía son las reglas para 7, 13, ... Pascal (matemático francés del siglo XVII) dio la regla para hallar caracteres de divisibilidad para cualquier número.
domingo, 15 de marzo de 2015
ARITMETICA - Introducción a la teoría de los números
LOS ENIGMAS DE LA TEORIA DE LOS NUMEROS
Muchos problemas sobre números primos y más en general los referentes a los números enteros, se caracterizan por la simplicidad de sus enunciados y por la dificultad increíble de su resolución. El gran matemático Gauss (1777-1855), enamorado de su belleza inaccesible llegó a decir que "la matemática es la reina de las ciencias y la teoría de los números la reina de las matemáticas". He aquí algunos ejemplos famosos de problemas obsesionantes: 1. El matemático Goldbach observó a mediados del siglo XVIII que cualquier número puede ser representado por la suma de dos números primos. Por ejemplo: 4 = 2 + 2, 6 = 3 + 3, 8 = 5 + 3, 10 = 5 + 5, 12 = 5 + 7, ..., 100 = 97 + 3, etc. Propuesto este problema a Euler, matemático máximo de aquella centuria, sigue hoy sin resolver afirmativa o negativamente, a pesar de los esfuerzos de geniales matemáticos y de los poderosos instrumentos puestos en juego. Ningún progreso importante se habla logrado en dos siglos hasta que en 1931 el malogrado matemático ruso Schnirelmann (1905-1938) dio una primera respuesta probando que todo entero positivo puede ser representado por la suma de no más de 300.000 números primos. Según Goldbach, bastan 2 primos para componer cualquier número; pero Schnirelmann necesitó nada menos que 300.000 sumandos primos, y, sin embargo, éste fue un gran progreso, pues abría un camino hacia la solución; otro gran salto ha dado recientemente Vinogradov: bastan 4 sumandos primos; esperemos la solución al apasionante problema. Se ha observado que frecuentemente se presentan números primos gemelos o consecutivos, es decir, de la forma n y n+2. Por ejemplo 3 y 5, 11 y 13, 29 y 31, etc. ¿Hay infinitos de estos pares de primos gemelos? Este problema aún no se ha resuelto. En la relación pitagórica a² + b² = c² hay grupos de números enteros tales como (3, 4, 5), (5, 12, 13), (7, 24, 25), etc., que la satisfacen. ¿Hay números enteros que satisfacen la relación a?+ b? = c? (n > 2)? Este es el celebérrimo teorema de Fermat (1601-1665), quien afirmó haberlo resuelto en forma negativa. Desde entonces el teorema ha desafiado a los sabios, que no han hallado aún la solución afirmativa ni negativa. La Academia de Ciencias de Gottingen fue encargada de adjudicar un premio de 100.000 marcos oro a quien lo resolviera. Puede imaginarse la lluvia torrencial de pretendidas soluciones, enviadas por los aficionados de todo el orbe; pero el enigma sigue inextricable.
sábado, 14 de marzo de 2015
ARITMETICA - Introducción a la teoría de los números
DIVISORES COMUNES A VARIOS NUMEROS. MAXIMO COMUN DIVISOR
Para hallar divisores de un solo número basta tomar algunos de sus factores primos y elevarlos a cualquier exponente que no exceda al exponente que tiene cada factor en el número. Si tratamos ahora de hallar divisores comunes a varios números, por ejemplo:
2520 = 2³ . 3² . 5 . 7 900 = 2² . 3². 5² 2970=2 . 3³ . 5 . 11
Es decir, divisores de todos ellos simultáneamente, claro es que habrá que formar productos formados tan sólo por los factores contenidos en todos ellos; es decir, por los factores comunes, 2, 3, 5 y poniendo a cada factor un exponente que no exceda al que tiene, en ninguno de los números dados. Serán divisores comunes de los números dados los siguientes:
2 . 3 = 6 3² . 5 = 45 2 . 3² . 5 = 90
En cambio el número 2 . 3 . 7 = 42 no es divisor de todos porque en él figura el factor primo 7, que no está en el número 900 ni en el 2970. Análogamente, el 3² . 11 = 99 no es divisor común por tener el factor 11 no contenido en 2520 ni en 900. El número 2 . 3³ . 5 = 270 tampoco es divisor común, pues a pesar de que todos sus factores primos 2, 3, 5, son comunes a los números dados, el exponente de 3³ supera al de 3², con que este factor primo 3 figura en los números 900 y 2520. Asimismo ningún número conteniendo potencias de 2 y de 5 de exponentes mayores que 1 sería divisor común.
Entre todos estos divisores comunes que se pueden formar, ¿cuál es el mayor de todos? Será el que tenga todos los factores primos, comunes, 2, 3, 5, cada uno elevado al menor exponente con que figura en los números dados, o sea 2 . 3² . 5. En efecto, no puede formarse un divisor común mayor, pues o tendría los mismos factores elevados a exponentes mayores, o tendría algún factor primo nuevo, lo cual es imposible. Este número es, pues, el mayor divisor común de los números dados, llamado usualmente máximo común divisor, y expresado en abreviatura así: m.c.d. Aunque no precisa más definición, conviene repetir:
Máximo común divisor de varios números es el mayor de los números que son divisores de todos ellos. Cuando un número divide a otros varios, es el m.c.d. de todos ellos y de si mismo.
viernes, 13 de marzo de 2015
ARITMETICA - Introducción a la teoría de los números
LA DIVISIBILIDAD Hemos visto dos clases de división: la exacta y la entera. Hay ocasiones en las que no interesa el cociente, sino solamente importa saber si la división es exacta o inexacta.
DIVISIBILIDAD POR 2. — Los múltiplos de 2 hasta 10 son 2, 4, 6, 8, 10. Para reconocer si un número mayor que 10 es par, descompongámoslo en dos partes separando las decenas de las unidades, por ejemplo:
4.825 = 4.820 + 5 378 = 370 + 8 etc.
Las decenas constituyen un número múltiplo de 10 y, por tanto, de 2; el número dado será, pues, par cuando las unidades sean pares o cuando no las haya. La condición para que un número sea par es que la cifra de las unidades sea cero o cifra par. Por ejemplo: 378 es par; 4 825 es impar.
DIVISIBILIDAD POR 5. — Análogamente, los múltiplos de 5 hasta 10 son 5 y 10. Dado un número cualquiera mayor que 10, se puede imaginar descompuesto en sus decenas y unidades. Aquéllas constituirán un múltiplo de 5; bastará, pues, observar éstas, y así resulta: La condición para que un número sea divisible por 5 es que termine en cero o en cinco.
DIVISIBILIDAD POR 4 Y POR 25. — Para averiguar si un número cualquiera es o no es divisible por 4 ó 25 imaginémosle descompuesto en sus centenas de una parte y en sus decenas y unidades de otra. Así,
346 = 300 + 46 6.375 = 6.300 + 75 etc.
346 soldados no pueden formar de a cuatro, porque agrupados en 3 compañías de a cien y 46 soldados, aquéllos podrían formar de a cuatro, pero estos soldados sobrantes no. Análogamente: La condición para que un número sea divisible por 8 ó por 125 es que las tres últimas cifras del número sean ceros o constituyan un múltiplo de dicho divisor.
DIVISIBILIDAD POR 3 Y POR 9. — Ante todo se comprueba fácilmente que los números 9, 99, 999, 9.999, etcétera, son divisibles por 3 y por 9. Tratemos de averiguar si por ejemplo el número 6.348 es divisible por 3 y es divisible por 9. Escribámoslo así:
La condición para que un número sea divisible por 3 ó por 9 es que lo sea la suma de las cifras que lo forman. Así, el número 6.348 es divisible por 3, por serlo la suma 6 + 3 + 4 + 8 = 21. En cambio no es divisible por 9 por no serlo 21.
jueves, 12 de marzo de 2015
ARITMETICA - Introducción a la teoría de los números
LOS NUMEROS PRIMOS
Las docenas se embalan más cómodamente que las decenas. Así, por 12ejemplo, botellas pueden encajonarse de tres modos: 1 fila de 12; 2 filas de 6 y 3 filas de 4. En cambio, 10 objetos sólo pueden disponerse en una fila de a 10 ó en dos filas de a 5. Peor todavía es el caso para 13 objetos, pues sólo pueden disponerse en una fila de a 13, y de cualquier otro modo que se ensaye su colocación para encajonarlos, es decir, para formar rectángulo, siempre sobra o falta algún objeto, como indican esquemáticamente las figuras:
La razón es bien sencilla: el número 13 no puede descomponerse en factores más que de un solo modo: 1 x 13, es decir, no admite más divisores que él mismo y la unidad. Tales números tienen interés especial como los elementos en Química y han recibido el nombre de números primos o simples. Un número se llama PRIMO O SIMPLE cuando no admite ningún divisor distinto de sí mismo y de 1.
Ejemplos: El número 2 es primo porque el único número menor que él es 1. El número 3 también es primo, porque el único número menor que él y distinto de 1 es 2, y 3 no es divisible por 2; del mismo modo ningún número par distinto de 2 es primo. El 5, en cambio, es primo, pues no es divisible por 2 ni por 3 ni por 4. El 7 también es primo. El 9 no, por ser múltiplo de 3. El 11 sí, etc.
Cabe preguntar: ¿Cuántos números primos hay? Desde muy antiguo se ha probado que no hay un número limitado de números primos. Hallado uno, por muy grande que sea, existe siempre otro mayor, y, por tanto, no terminaríamos nunca de contarlos. Se expresa esto abreviadamente diciendo: La sucesión de números primos es ilimitada.
miércoles, 11 de marzo de 2015
ARITMETICA - Introducción a la teoría de los números
CURIOSAS PARTICULARIDADES DE LOS NUMEROS
Hay números, como 14, que presentan la característica de que la suma de sus factores 1, 2 y 7 no alcanza al número. Números de este tipo se llaman excesivos. Hay otros, como el 12, que resultan inferiores a la suma de sus factores: 1 + 2 + 3 + 4 + 6 = 16 y que se llaman deficientes. Existen además otros números llamados perfectos, que tienen la notable particularidad de ser exactamente iguales a la suma de sus divisores. Así por ejemplo: 6 = 1 + 2 + 3 28 = 1 + 2 + 4 + 7 + 14 Los pitagóricos creían que nada puede ser concebido ni conocido si no tiene número y asignaban a estos números perfectos virtudes especiales. San Agustín (354-430) escribió: "6 es un número perfecto en sí mismo, y no porque Dios creó todas las cosas en 6 días; más bien la recíproca es cierta. Dios creó todas las cosas en 6 días porque este número es perfecto, y sería perfecto aunque el trabajo de los 6 días no hubiera existido." Los números amigos son tales que la suma de los divisores de cada uno es exactamente igual al otro. Ejemplo: 284 tiene los divisores 1, 2, 4, 71, 142, cuya suma es 220, y 220 tiene los divisores 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, cuya suma es 284.
martes, 10 de marzo de 2015
ARITMETICA - Introducción a la teoría de los números
LA CRIBA DE ERATOSTENES. TABLAS DE NUMEROS PRIMOS
Puesto que no es posible conocer todos los números primos, estudiemos siquiera el modo de obtener ordenadamente todos aquellos que sean menores que un cierto número, por ejemplo, 100. El procedimiento consiste en escribir los números 1 a 100 y suprimir metódicamente todos los números que no sean primos. En primer lugar habrá que suprimir los pares, excepto el 2, que es el único par primo; por tanto, será más breve empezar escribiendo solamente el 2 y los impares, así:
Suprimidos a partir del 3 contando de 3 en 3 los múltiplos 9, 15, 21, 27, ... después los múltiplos de 5 (25, 35, ...) y los múltiplos de 7 (21, ...), quedan estos números:
Tratemos ahora de suprimir los múltiplos de 11. Claro es que los productos de 11 por números menores que 11 se han suprimido ya al tachar los múltiplos de dichos números; por tanto, sólo hay que comenzar por los productos 11, por el mismo 11 o por factores mayores; y como 11 x 11 es mayor que 100, resulta que en la tabla no queda ningún múltiplo de 11, ni tampoco de ningún número mayor que 11 por análoga razón. Es decir, todos los números que quedan después de suprimidos los múltiplos de 2, 3, 5 y 7 son primos. Esta es la famosa criba de Eratóstenes, así llamada porque la tradición atribuye a este matemático griego el haber seguido idéntico procedimiento, unos 200 años antes de Jesucristo, grabando los números en una placa de cobre, y agujereando los lugares de los números no primos, con lo que, después de efectuadas estas operaciones, la placa quedó convertida en una criba. Es la primera tabla de números primos que registra la Historia.
Notas: 1) Por definición, todo número no primo admite por lo menos un divisor distinto del mismo número y de 1. Si este divisor no es primo, admitirá otro; si éste tampoco lo es, admitirá otro. Como los divisores son cada vez menores, siguiendo así, llegaremos a un número que no tendrá más divisor que 1 ó él mismo, el cual será, por tanto, primo y divisor de todos los demás. Luego: Todo número no primo admite un divisor primo. 2) Para probar que cualquiera que sea la prolongación dada a la tabla de números primos, existe siempre otro primo mayor, imaginemos formado el producto P de todos los números de la tabla y añadámosle 1. Si el número resultante P+1 es primo, el teorema está demostrado, y si no lo es, admitirá algún divisor primo que no puede ser de la tabla, y será, por tanto, mayor (pues siendo P un múltiplo de todos los números de la tabla, al dividir P+1 por dichos números, se obtendrá en todos resto 1).
lunes, 9 de marzo de 2015
ARITMETICA - Introducción a la teoría de los números
LOS NUMEROS COMPUESTOS
DESCOMPOSICION DE UN NUMERO COMPUESTO EN FACTORES PRIMOS. — Apliquemos por ejemplo a 315 la regla anterior, ensayando sucesivamente los divisores primos 2, 3, 5, 7, ... La primera división exacta se obtiene con el 3 y el cociente es 105; de modo que podemos escribir:
315 = 3 . 105
Apliquemos al factor 105 el mismo procedimiento; comenzaremos, pues, por el 3, dando de cociente 35; de modo que 105 = 3 . 35, y, por tanto,
315 = 3 . 3 . 35
El número 35 ya no es divisible por 3; en cambio, lo es por el número primo siguiente, 5; 35 = 5 . 7, el cociente 7 es primo. Resumen:
315 = 3 . 3 . 5 . 7 = 3² . 5 . 7
El proceso anterior es aplicable a cualquier número compuesto. Todo número compuesto es un producto de factores primos.
Ejemplos: Dados los números 546 y 3 960, la operación se dispone prácticamente así:
Colocando una raya vertical a la derecha del número, los divisores se colocan sucesivamente a la derecha de la raya, en columna y cada uno debajo del anterior. Se obtiene de este modo:
546 = 2 . 3 . 7 . 13 3.960 = 2³ . 3³. 5 . 11
METODO RAPIDO. — Cuando se ve inmediatamente una descomposición del número en dos o más factores, conviene aprovecharla, descomponiendo cada uno en factores primos. Así, por ejemplo:
3600 = 36 . 100 = 4 . 9 . 10² = 2² . 3² . 2² . 5² = 2(4) . 3² . 5²
Hágase como se haga, la descomposición en factores resulta siempre la misma; es decir, se obtendrán siempre los mismos factores y cada uno de ellos elevado a los mismos exponentes. Esto se expresa diciendo: Cada número compuesto no admite más que una descomposición en factores primos.
domingo, 8 de marzo de 2015
ARITMETICA - Introducción a la teoría de los números
LOS NUMEROS COMPUESTOS
DEFINICION Y CRITERIO PARA RECONOCERLOS. — Todo número que no es primo, es decir, todo número que admite algún divisor distinto de sí mismo y de la unidad, se llama compuesto. Son, pues, compuestos todos los números pares, excepto el 2. Son también compuestos, por ejemplo, 453 (divisible por 3), 725 (por 5), 627 (por 11), etc. Si el número verifica alguno de los caracteres de divisibilidad estudiados se reconoce en seguida que es compuesto, como en los ejemplos que preceden. En caso contrario, ¿hará falta ensayar si el número es divisible por todos los números menores que él? Si se dispone de una tabla de números primos, para todo número comprendido dentro del límite de la tabla, ella nos da el trabajo hecho, pues bastará ver si el número en cuestión está o no está en la tabla. Con la tabla de los números primos a la vista reconocemos que los números 229, 557 y 823 son primos, y que los 289, 437 y 703 son compuestos. Si el número dado supera al límite de la tabla de que se dispone, aplicaremos esta regla:
Para reconocer si un número es primo o compuesto, divídase por los números primos sucesivos 2, 3, 5, 7, 11, …; si se llega hasta un cociente igual o menor que el divisor sin haber obtenido ninguna división exacta, el número es primo, y en caso contrario, compuesto.
En efecto, un número de objetos es primo cuando no se pueden embalar en rectángulo de varias filas y columnas. Para ver si un número es primo o compuesto bastará, pues, ver si se pueden distribuir tales objetos en cuadro. Sean, por ejemplo, 53 objetos y ensayemos su ordenación en columnas de a 3:
Al llegar a este punto se ve la inutilidad de proseguir los ensayos, pues habiendo resultado hasta ahora rectángulos alargados en un sentido y habiéndose llegado, por último, a formar inútilmente un cuadro de 7 filas por 7 columnas, si continuáramos probando con columnas de más objetos, las filas serían más cortas, y como girando el rectángulo o cajón las filas pueden convertirse en columnas, sería tanto como volver a repetir los ensayos infructuosos va efectuados.
sábado, 7 de marzo de 2015
MATEMATICA – Geometría elemental
NACIMIENTO DE LA CIENCIA GEOMETRICA
La geometría es sin duda uno de los frutos más perfectos del raciocinio humano. Desde la antigüedad más remota, el hombre, que impulsado por la necesidad de resolver problemas de orden práctico, supo aquilatar las ventajas de obtener resultados generales (aplicables a casos concretos diversos) operando, no directamente sobre los objetos naturales, sino sobre abstracciones de esos mismos datos empíricos, creó las bases de la Geometría. Entre los babilonios y los egipcios, que en razón del progreso de su agricultura y de su comercio, de su arte para el riego y la arquitectura, debieron ingeniarse para medir y calcular superficies y volúmenes, se encontraron los primeros geómetras de la antigüedad. Los problemas que planteaban las periódicas inundaciones del río Nilo, fueron el incentivo que obligó a los egipcios a resolver cuestiones que todavía hoy nos asombran. Sin embargo, la geometría de babilonios y egipcios era aún una ciencia eminentemente experimental. Sólo cuando los frutos de su técnica bastante avanzada pasaron a Grecia, diestra ya en el uso de la razón y ejercitada por las especulaciones filosóficas, llegaron a constituir una ciencia lógica. Tales de Mileto, que vivió en el siglo VI antes de Cristo, fue el primer gran geómetra griego cuyo nombre haya sido recogido por la Historia. La Geometría, que empezó a desarrollarse como ciencia en Grecia, con Tales y su escuela, sobre la base de los conocimientos adquiridos por otros pueblos, se enriqueció con nuevos e importantes aportes; y es esencial destacar que el desarrollo griego de la Geometría se realizó en el plano de la especulación lógica. No se puede hablar de la Matemática en Grecia sin mencionar el nombre de Pitágoras. El y sus discípulos realizaron descubrimientos fundamentales, para el estudio de las relaciones numéricas entre las medidas lineales, áreas y volúmenes. Siglos más tarde, alrededor del año 300 antes de Cristo, y poco después que Aristóteles, vivió Euclides de Alejandría, que sistematizó y perfeccionó los descubrimientos de sus antecesores (Hipócrates de Quío, Eudoxio,...). Los Elementos de Euclides y la Lógica de Aristóteles son las únicas obras científicas que han resistido el embate de 22 siglos de progreso.
viernes, 6 de marzo de 2015
TE INVITO A VISITAR MI PAGINA SI ES DE SU PREFERENCIA DALE ME GUSTA
https://www.facebook.com/eddyedsus1
MATEMATICA – Triángulos
LA ESCUADRA Y EL MOVIMIENTO DE TRASLACION Toda lámina de cualquier material sólido cuya forma sea un triángulo rectángulo recibe el nombre de escuadra. También se llama así el instrumento formado por dos reglas perpendiculares.
Como en todo triángulo rectángulo, el lado opuesto al ángulo recto se llama hipotenusa, y los lados opuestos a los ángulos agudos, catetos. Con la escuadra se pueden trazar con mucha facilidad rectas paralelas. Sí se coloca como guía la regla en la forma que indica la figura, para trazar una paralela a la recta r que pase por un punto A no habrá más que correr la escuadra hasta la segunda posición y trazar r'.El movimiento de la escuadra se llama traslación. Podemos decir por consiguiente que las rectas paralelas son las posiciones de una misma recta móvil en una traslación.
Los carpinteros acostumbran a trazar paralelas utilizando un lápiz y apoyando los dedos sobre el borde de una tabla que le sirve, pues, de guía. Al mover la mano se va trazando la paralela. Más precisión se obtiene utilizando un gramil o taquito de madera (escantillón).
jueves, 5 de marzo de 2015
MATEMATICA – Geometría elemental
MEDIDA DE ANGULOS Y DE ARCOS
Para saber si dos ángulos convexos son iguales, haremos coincidir sus vértices y uno de sus lados viendo si coinciden los otros.
Si esto no es posible y se hace que los lados no coincidentes b y b' quedenen la misma región respecto del lado común a, caben dos posibilidades: el lado b queda dentro del ángulo a'b' y decimos entonces que el ángulo a'b' es mayor que ab y se escribe a'b' > ab; o bien el lado b queda fuera del ángulo a'b' y se escribe a'b' < ab. En el primer caso se dice que:
a'b' = ab + bb'
Y en el segundo:
ab = a'b' + b'b
Se puede, pues, definir la igualdad, la desigualdad y la suma. Tales entes se llaman magnitudes y serán estudiados más adelante; tenemos, pues, dos tipos de magnitudes: segmentos y ángulos. Se llama medida la representación de las magnitudes por números, de modo tal que se conserve la igualdad y la suma; más adelante nos ocuparemos de las longitudes, áreas y volúmenes. Ahora veamos cómo se miden los ángulos, que tienen la ventaja de ofrecer una unidad natural, que es el ángulo recto R, o bien una parte alícuota del mismo. Generalmente se adopta como unidad el ángulo que resulta de dividir el ángulo recto R en 90 partes iguales. A su vez este ángulo unidad, que se llama grado, tiene 60 minutos y cada minuto tiene 60 segundos. Este sistema se llama sexagesimal. La notación es: 35° 37' 16". Hay otro sistema, no tan difundido, que se llama centesimal, en el cual cada ángulo recto tiene 100 grados, cada grado 100 minutos y cada minuto 100 segundos. La notación es: 29° 87' 16". Sería muy incómodo medir un ángulo por comparación directa con un ángulo unidad, pero se salva esta dificultad midiendo los arcos correspondientes a los ángulos. Si desde los vértices de ángulos iguales, trazamos circunferencias con radios iguales, y consideramos los arcos limitados por los lados de los ángulos, la intuición nos dice que son iguales. Esta es la propiedad que utilizamos para la construcción de un ángulo igual a otro dado. Cuando se dice que un arco es de 30° se quiere significar que el ángulo correspondiente mide 30°.
Los instrumentos usados para medir ángulos en realidad miden arcos señalados sobre un disco circular. La figura muestra un transportador o limbo, en el que las divisiones corresponden a 1°. Existen otros divididos de minuto en minuto, y aun en diez segundos según sea el instrumento. Los usados en topografía aprecian 1'; en las observaciones astronómicas se llega a fracciones de 1".
miércoles, 4 de marzo de 2015
MATEMATICA - Función exponencial y función logarítmica
POTENCIAS DE EXPONENTE FRACCIONARIO, NULO O NEGATIVO
Si consideramos la expresión ?v a? con a positivo, observamos que elevada a la potencia n nos da a?. Pero si atribuimos a las potencias de exponente fraccionario las mismas reglas de las potencias con exponente entero debe ser:
Esto nos induce a considerar como lógico definir las potencias de exponente fraccionario en la siguiente forma:
POTENCIA DE EXPONENTE CERO: Aplicando la segunda regla a a?/a? igual a 1, resulta a?-?. Parece, pues, natural convenir en dar al símbolo aº el valor 1, para que se conserven las reglas de cálculo. Por definición será:
aº = 1
POTENCIA CON EXPONENTE NEGATIVO: Conviene adoptar el símbolo a-? para representar a 1/a?, pues al multiplicar a-?.a? resulta, en virtud de la primera regla, aº = 1, igualdad que acabamos de admitir. Por consiguiente por definición será:
a-? = 1/a?
Y en general
martes, 3 de marzo de 2015
MATEMATICA - La proporcionalidad y sus aplicaciones aritméticas
RAZONES Y PROPORCIONES ENTRE NUMEROS ABSTRACTOS
Se llama razón de dos números abstractos a su cociente indicado. Se llama proporción a la igualdad de dos razones. Utilizando letras en lugar de números, podemos escribir la proporción en las dos formas indicadas:
a : b = c : d
a y c: antencedentes b y d: consecuentes
a / b = c / d
b y c: medios a y d: extremos
Invirtiendo las dos razones:
b / a = d / c
Permutando los medios:
a / c = b / d
Permutando los extremos:
d / b = c / a
Puesto que el cociente a : b es igual a c : d, al multiplicar por el divisor b deberá obtenerse el dividendo a; es decir,
a = (c/d) . b = (c . b) / d
Y multiplicando otra vez por d se tiene:
a . d = c . b
Estas últimas igualdades se expresan diciendo que en toda proporción:
El producto de los extremos es igual al producto de los medios. Un extremo es igual al producto de los medios dividido por el otro extremo. Análogamente: Un medio es igual al producto de los extremos dividido por el otro medio.
Si varias razones son iguales y es k su valor, es decir:
a/a' = b/b' = c/c' = k
O sea:
a = a'k , b = b'k , c = c'k
Se deduce sumando estas igualdades:
a/a' = b/b' = c/c' = (a + b + c) / (a' + b' +c')
En palabras: En una serie de razones iguales la suma de los antecedentes es a la suma de los consecuentes, como un antecedente cualquiera es a su consecuente.
lunes, 2 de marzo de 2015
MATEMATICA - La proporcionalidad y sus aplicaciones aritméticas
LA PROPORCIONALIDAD INVERSA Y DE PROPORCIONALIDAD COMPUESTA
Si para realizar un trabajo tardo un mes dedicando 4 horas por día, es evidente que de trabajar 8 horas por día tardaría medio mes. Es decir que cuando aumento mi jornada de trabajo, disminuyo el número de días que empleo en efectuar ese trabajo, en forma tal que si trabajo el doble por día, tardo la mitad en realizarlo. Se dice entonces que en la correspondencia entre el número de horas que trabajo por día y el número de días que invierto en el trabajo hay una proporcionalidad inversa. (Como en los ejemplos de proporcionalidad directa, es claro que esta relación es válida dentro de ciertos límites, pues si trabajara 24 horas diarias, no tardaría 5 días, porque me agotaría mucho antes.) En general: dos magnitudes se llaman inversamente proporcionales cuando hay una correspondencia tal, que a cada cantidad de una corresponde una cantidad de la otra, y al multiplicar una cantidad por un número, la cantidad correspondiente queda dividida por el mismo número. Utilizando la noción de razón diremos: Dos magnitudes son inversamente proporcionales cuando la razón de dos cantidades cualesquiera de una es igual a la razón inversa de las dos cantidades correspondientes de la otra. En nuestro ejemplo: 4 / 8 = 15 / 30
LA PROPORCIONALIDAD COMPUESTA. - Si se debe construir un muro, el número de días necesarios para ello depende de la longitud, ancho y altura del muro, del número de obreros y de la jornada de trabajo. En este caso se dice que existe una proporcionalidad compuesta. Suponiendo fijas todas las magnitudes, excepto una, se observa si el número de días es directa o inversamente proporcional a esa magnitud que se deja variable. Así resulta que el número de días necesarios para construir el muro es:
directamente proporcional a la longitud del muro directamente proporcional al ancho del muro directamente proporcional a la altura del muro inversamente proporcional al número de obreros inversamente proporcional al número de horas de trabajo diario
domingo, 1 de marzo de 2015
ARITMETICA - Los números y la numeración
EL VALIOSO CERO
La tercera característica de nuestro sistema decimal de numeración está dada por el signo 0, de importancia excepcional, porque permite escribir muy simplemente y sin ambigüedad cualquier número, por grande que sea, con estas solas cifras: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Sin el cero, que viene a ocupar los lugares vacantes, no sería posible la representación escrita de todos los números; sin embargo no interviene en la numeración oral. En ella se distinguen perfectamente estos números:
Tres millones cuatro mil ocho Tres mil cuatro cientos ocho Tres mil cuarenta y ocho
Pero si escribiéramos las tres cifras 348 no se sabría a cuál de ellos nos referimos. En cambio, mediante el cero, desaparece toda ambigüedad, escribiendo respectivamente:
3.004.008 3.408 3.048
Nuestra palabra cifra viene de cefer, que significaba cero; ésta es la cifra por antonomasia. El gran matemático Pedro Simón de Laplace (1749-1827) tenía razón (salvo en dar por cierto su origen hindú) cuando escribía: "Ha sido la India quien nos legó el ingenioso método de expresar todos los números por medio de diez símbolos, recibiendo cada símbolo un valor de posición y un valor absoluto; una idea profunda e importante que nos resulta ahora tan simple, hasta el punto de ignorar su verdadero mérito. Pero su gran simplicidad y la gran comodidad con que auxilia todos los cálculos ha colocado a nuestra aritmética en la primera fila de las invenciones útiles; y apreciaremos mejor la magnitud de esta adquisición si recordamos que ella escapó al genio de Arquímedes y Apolonio, dos de los más grandes hombres producidos por la antigüedad."
En el cuadro anterior, para el caso del número 370.504.982.367.045.102.647.538 se han indicado las denominaciones correspondientes a cada cifra. La lectura debe comenzarse por las unidades de orden más elevado.